Problema de Ramanujan de radicales anidados
El viernes pasado, John D. Cook escribió el artículo Ramanujan’s nested radical en el que comenta el siguiente problema planteado por Ramanujan en el Journal of Indian Mathematical Society:
¿Cuál es el valor de la siguiente expresión?
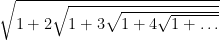
A partir del problema he elaborado la siguiente relación de ejercicios en Haskell para la asignatura de Informática (de 1º del Grado en Matemáticas).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
-- --------------------------------------------------------------------- -- Librerías auxiliares -- --------------------------------------------------------------------- import Graphics.Gnuplot.Simple -- --------------------------------------------------------------------- -- Ejercicios -- --------------------------------------------------------------------- -- --------------------------------------------------------------------- -- Ejercicio 1. Definir la función -- ramanujan :: Double -> Double -- tal que (ramanujan n) es el n-ésimo término de la sucesión de -- Ramanujan correspondiente a la expresión -- sqrt(1+2*sqrt(1+3*sqrt(1+4*sqrt(1+...)))) -- es decir, -- ramanujan(1) = 1 -- ramanujan(2) = sqrt(1+2) -- ramanujan(3) = sqrt(1+2*sqrt(1+3)) -- ramanujan(4) = sqrt(1+2*sqrt(1+3*sqrt(1+4))) -- Por ejemplo, -- ramanujan 4 == 2.559830165300118 -- --------------------------------------------------------------------- -- 1ª solución: ramanujan :: Double -> Double ramanujan n = f [2..n] where f [] = 1 f (x:xs) = sqrt (1 + x * f xs) -- 2ª solución: ramanujan2 :: Double -> Double ramanujan2 n = aux n where aux 1 = n aux m = (n-m+1) * sqrt (1 + aux (m-1)) -- --------------------------------------------------------------------- -- Ejercicio 2. Definir la función -- limite :: (Num a, Enum a, Num b, Ord b) => (a -> b) -> b -> b -- tal que (limite f a) es el valor de f en el primer término x tal que -- para todo y entre x+1 y x+100, el valor absoluto de f(y)-f(x) es -- menor que a. Por ejemplo, -- limite (\n -> (2*n+1)/(n+5)) 0.001 == 1.9900110987791344 -- limite (\n -> (1+1/n)**n) 0.001 == 2.714072874546881 -- --------------------------------------------------------------------- limite :: (Num a, Enum a, Num b, Ord b) => (a -> b) -> b -> b limite f a = head [f x | x <- [1..], maximum [abs(f y - f x) | y <- [x+1..x+100]] < a] -- --------------------------------------------------------------------- -- Ejercicio 3. Calcular el límite de la sucesión de Ramanujan con una -- aproximación de 10^(-20). -- --------------------------------------------------------------------- -- El cálculo es -- ghci> limite ramanujan 1e-20 -- 3.0 -- --------------------------------------------------------------------- -- Ejercicio 4. Definir la función -- dibujoRamanujan :: Double -> IO () -- tal que (dibujoRamanujan n) dibuja los n primeros términos de la -- sucesión de Ramanujan. Por ejemplo, con (dibujoRamanujan 20) se -- obtiene la figura 1 (en el final de la entrada). -- --------------------------------------------------------------------- dibujoRamanujan :: Double -> IO () dibujoRamanujan n = plotList [] [(m,ramanujan m) | m <- [1..n]] -- Para dibujarla en el fichero Ramanujan.png dibujoRamanujan2 :: Double -> IO () dibujoRamanujan2 n = plotList [Title "Sucesion de Ramanujan", PNG "Ramanujan.png", YLabel "Ramanujan(n)", Key Nothing] [(m,ramanujan m) | m <- [1..n]] |
