I1M2012 – Página 14

I1M2012: Ordenación por mezcla

PorJosé A. Alonso 27 noviembre 20128 marzo 2013

En la segunda parte de la clase de hoy de Informática de 1º del Grado en Matemáticas hemos comentado las soluciones de los ejercicios de la 8ª relación que tratan de la ordenación por mezcla.

Los ejercicios, y sus soluciones, se muestran a continuación:
Read More “I1M2012: Ordenación por mezcla”

I1M2012: Sumas de factoriales que dan cuadrados perfectos

PorJosé A. Alonso 27 noviembre 20128 marzo 2013

En la primera parte de la clase de hoy de Informática de 1º del Grado en Matemáticas hemos comentado la solución con Haskell de un problema propuesto en la revista Mathematics Magazine. Su enunciado es

Encontrar todos los enteros positivos m y n para los que se
cumpla que: $1!+2!+3!+ \dots +n!=m^2$ .

Su traducción directa es

sol :: [(Integer,Integer)]
sol = [(n,m) | n <- [1..], m <- [sumaFactoriales n], esCuadrado m]

1 2	sol :: [(Integer,Integer)] sol = [(n,m) \| n <- [1..], m <- [sumaFactoriales n], esCuadrado m]

o, usando let,

sol' :: [(Integer,Integer)]
sol' = [(n,m) | n <- [1..], let m = sumaFactoriales n, esCuadrado m]

1 2	sol' :: [(Integer,Integer)] sol' = [(n,m) \| n <- [1..], let m = sumaFactoriales n, esCuadrado m]

donde

(sumaFactoriales n) es la suma de los factoriales de 1 a n

Haskell

sumaFactoriales :: Integer -> Integer sumaFactoriales n = sum [factorial x | x <- [1..n]]

1
2

sumaFactoriales :: Integer -> Integer
sumaFactoriales n = sum [factorial x | x <- [1..n]]
(factorial n) es el factorial de n.

Haskell

factorial :: Integer -> Integer factorial n = product [1..n]

1
2

factorial :: Integer -> Integer
factorial n = product [1..n]
(esCuadrado x) se verifica si x es un cuadrado perfecto.

Haskell

esCuadrado :: Integer -> Bool esCuadrado x = x == y*y where y = floor (sqrt (fromIntegral x))

1
2
3

esCuadrado :: Integer -> Bool
esCuadrado x = x == y*y
where y = floor (sqrt (fromIntegral x))

Con esta definición se encuentran las siguientes soluciones

ghci> sol
[(1,1),(3,9)  
C-c C-c
Interrupted.

ghci> sol

[(1,1),(3,9)

C-c C-c

Interrupted.

Se observa que después de calcular las dos primeras sigue buscando por lo que hay que terminar el cálculo (con C-c C-c) sin encontrar más soluciones.

Que las dos primeras son soluciones se comprueba fácilmente:

$1! = 1 = 1^2$
$1!+2!+3! = 9 = 3^2$ .

Vamos a investigar porqué no hay más soluciones. Para ello, empezamos calculando las sumas de los factoriales

ghci> [sumaFactoriales n | n <- [1..10]]
[1,3,9,33,153,873,5913,46233,409113,4037913]

1 2	ghci> [sumaFactoriales n \| n <- [1..10]] [1,3,9,33,153,873,5913,46233,409113,4037913]

Se observa que, a partir de la cuarta, todas terminan en 3. Por otra parte, calculando los cuadrados de los dígitos

ghci> [x^2 | x <- [0..9]]
[0,1,4,9,16,25,36,49,64,81]

1 2	ghci> [x^2 \| x <- [0..9]] [0,1,4,9,16,25,36,49,64,81]

se observa que ninguno termina en 3; es decir, ningún cuadrado perfecto temina en 3.

Para terminar, nos falta demostrar la conjetura anterior (si n>3, entonces $1!+2!+3!+ \dots +n!$ termina en 3). Para ello calculamos los primeros factoriales

ghci> [factorial n | n <- [1..10]]
[1,2,6,24,120,720,5040,40320,362880,3628800]

1 2	ghci> [factorial n \| n <- [1..10]] [1,2,6,24,120,720,5040,40320,362880,3628800]

Se observa que para n=4 termina en 3 (es 1+2+6+24=33) y que, para n>4, el último dígito de n! es 0 (que es fácil de demostrar ya que si n>4, entre los factores de n están el 2 y el 5).

I1M2012: Ejercicios de definiciones por recursión (2)

PorJosé A. Alonso 26 noviembre 20128 marzo 2013

En la clase de hoy de Informática de 1º del Grado en Matemáticas hemos comentado las soluciones a los 6 últimos ejercicios de la 7ª relación, que tratan sobre definiciones por recursión.

Los ejercicios, y sus soluciones, se muestran a continuación:
Read More “I1M2012: Ejercicios de definiciones por recursión (2)”

I1M2012: Ejercicios de definiciones por recursión en Haskell

PorJosé A. Alonso 22 noviembre 20128 marzo 2013

En la clase de hoy de Informática de 1º del Grado en Matemáticas hemos comentado las soluciones a los 7 primeros ejercicios de la 7ª relación, que tratan sobre definiciones por recursión.

Los ejercicios, y sus soluciones, se muestran a continuación:
Read More “I1M2012: Ejercicios de definiciones por recursión en Haskell”

I1M2012: Último dígito del producto de números de Fermat

PorJosé A. Alonso 20 noviembre 20128 marzo 2013

En la segunda parte de la clase de hoy de Informática de 1º del Grado en Matemáticas hemos comentado la solución con Haskell de un problema propuesto para la Olimpiada Internacional de Matemáticas (IMO) de 1971. Su enunciado es

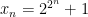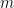Sea $x_n = 2^{2^n} + 1$ y sea $m$ el producto de $x_2, x_3, \dots, x_{1971}$ . Calcular el último dígito de $m$ .

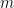La primera definición es la traducción directa del enunciado

sol1 :: Integer
sol1 = ultimo (product [x n | n <- [2..1971]])

1 2	sol1 :: Integer sol1 = ultimo (product [x n \| n <- [2..1971]])

donde (x n) es el n-ésimo término de la sucesión

x :: Int -> Integer 
x n = 2^(2^n) + 1

1 2	x :: Int -> Integer x n = 2^(2^n) + 1

y (ultimo x) es el último dígito de x

ultimo :: Integer -> Integer
ultimo x = rem x 10

1 2	ultimo :: Integer -> Integer ultimo x = rem x 10

Aunque la primera solución es simple, tiene un inconveniente: Haskell no puede calcular números tan grandes. Una estrategia para resolverlo es considerar casos menores y buscar alguna regularidad. Para ello, generalizamos la primera solución sustituyendo 1971 por una variable.

sol2 :: Int -> Integer
sol2 a = ultimo (product [x n | n <- [2..a]])

1 2	sol2 :: Int -> Integer sol2 a = ultimo (product [x n \| n <- [2..a]])

Con la 2ª definición calculamos el último dígito de los primeros productos

ghci> [sol2 a | a <- [2..20]] 
[7,9,3,1,7,9,3,1,7,9,3,1,7,9,3,1,7,9,3]

1 2	ghci> [sol2 a \| a <- [2..20]] [7,9,3,1,7,9,3,1,7,9,3,1,7,9,3,1,7,9,3]

Se observa que el resultado está formado por la repetición de los números 7, 9, 3 y 1. A partir de la observación conjeturamos una nueva definición

sol3 :: Int -> Integer
sol3 a | b == 2 = 7
       | b == 3 = 9
       | b == 0 = 3
       | b == 1 = 1
       where b = rem a 4

sol3 :: Int -> Integer

sol3 a | b == 2 = 7

| b == 3 = 9

| b == 0 = 3

| b == 1 = 1

where b = rem a 4

Podemos comprobar, para pequeños valores, que las 2 definiciones son equivalentes

ghci> [sol2 a | a <- [2..20]] == [sol3 a | a <- [2..20]] 
True

1 2	ghci> [sol2 a \| a <- [2..20]] == [sol3 a \| a <- [2..20]] True

Además, con la 3ª definición se puede calcular la solución del problema original

ghci> sol3 1971
9

1 2	ghci> sol3 1971 9

es decir, el último dígito del producto $x_2x_3 \dots x_{1971}$ es 9.

Para justificar la solución, hay que demostrar que la definición sol3 es correcta; es decir, que los últimos dígitos de los productos forman la sucesión 7, 9, 3, 1, 7, 9, 3, 1, 7, 9, 3, 1, 7, 9, 3, 1, 7, 9, 3, … Para ello, observamos el último dígito de los $x_n$

ghci> [ultimo (x n) | n <- [2..20]]
[7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7]

1 2	ghci> [ultimo (x n) \| n <- [2..20]] [7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7]

Se observa que todos son 7. Esto justifica la sucesión de los productos, ya que cada término es el último dígito del producto del anterior por 7. Además, permite una nueva definición de la solución por recursión

sol4 :: Int -> Integer
sol4 a | a == 2    = 7
       | otherwise = ultimo (7 * sol4 (a-1))

sol4 :: Int -> Integer

sol4 a | a == 2 = 7

| otherwise = ultimo (7 * sol4 (a-1))

Podemos comprobar, para pequeños valores, que es equivalente a la anterior

ghci> [sol3 a | a <- [2..20]] == [sol4 a | a <- [2..20]] 
True

1 2	ghci> [sol3 a \| a <- [2..20]] == [sol4 a \| a <- [2..20]] True

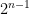Para terminar, sólo queda demostrar que si $n>1$ , entonces el último dígito de $2^{2^n} + 1$ es 7 o, equivalentemente, que el último dígito de $2^{2^n}$ es 6. Lo que se tiene ya que $2^{2^n} = 2^{2\cdot2^{n-1}} = (2^2)^{2^{n-1}} = 4^{2^{n-1}}$ . Además, como $n>1$ se tiene que $2^{n-1}$ es un número par mayor que 0 y, por tanto, el último dígito de 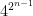$4^{2^{n-1}}$ es 6.