Biparticiones con igual suma que producto en Haskell

PorJosé A. Alonso

En Números y algo más … se ha planteado el siguiente problema

¿Es posible dividir todos los números del 1 al 2012 en dos grupos, S y P, tal que la suma de los números de S sea igual al producto de los números que están en P? ¿y si fueran 2011 ó 2013? Si es posible, ¿Cómo estarían formados esos conjuntos?

En la siguiente relación de ejercicios (elaborada para la asignatura de Informática de 1º del Grado en Matemáticas) se resuelve el problema con Haskell.
Read More “Biparticiones con igual suma que producto en Haskell”

El algoritmo de Moessner en Haskell

PorJosé A. Alonso

La presente relación de ejercicios está basada en el artículo El algoritmo de Moessner escrito por Antonio Roldán Martínez en su blog Números y hoja de cálculo.

El proceso de Moessner de orden n consiste en lo siguiente: De la lista de los números naturales, se tacha los elementos que ocupan las posiciones n, 2*n, … y se forma la sucesión de las sumas parciales de los restantes elementos. De la resultante sucesión se tacha los elementos que ocupan las posiciones n-1, 2*(n-1), … y se forma la sucesión de las sumas parciales de los restantes elementos. El proceso se repite n-1 veces. Por ejemplo, para n=2:

Se observa que los elementos de la última es la sucesión de los cuadrados. Para n=3, el proceso de Moessner es

Se observa que los elementos de la última es la sucesión de los cubos. Para n=4, el proceso de Moessner es

Se observa que los elementos de la última es la sucesión de los cuartas potencias. El teorema de Moessner afirma que para cualquier n, la sucesión obtenida mediante el proceso de Moessner es la de las potencias n-ésimas; es decir 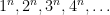1^n, 2^n, 3^n, 4^n, \dots

El objetivo de los siguientes ejercicios es definir en Haskell una función que simule el proceso de Moessner y comprobar el teorema.
Read More “El algoritmo de Moessner en Haskell”

Wave equation numerical resolution: a comprehensive mechanized proof of a C program

PorJosé A. Alonso

Se ha publicado un nuevo artículo de formalización en Coq: Wave equation numerical resolution: a comprehensive mechanized proof of a C program.

Sus autores son Sylvie Boldo, François Clément, Jean-Christophe Filliâtre, Micaela Mayero, Guillaume Melquiond y Pierre Weis.

El resumen del artículo es

We formally prove correct a C program that implements a numerical scheme for the resolution of the one-dimensional acoustic wave equation. Such an implementation introduces errors at several levels: the numerical scheme introduces method errors, and floating-point computations lead to round-off errors. We annotate this C program to specify both method error and round-off error. We use Frama-C to generate theorems that guarantee the soundness of the code. We discharge these theorems using SMT solvers, Gappa, and Coq. This involves a large Coq development to prove the adequacy of the C program to the numerical scheme and to bound errors. To our knowledge, this is the first time such a numerical analysis program is fully machine-checked.

El código correspondiente se encuentra en http://fost.saclay.inria.fr/wave_total_error.html

I1M2011: Libro de ejercicios resueltos de programación en Haskell (v. 30-May-12)

PorJosé A. Alonso

A lo largo del curso iré actualizando un libro de ejercicios resueltos de programación con Haskell con las relaciones de ejercicios del curso de Informática (de 1º del Grado en Matemáticas)

En la versión actual contiene las soluciones de las 33 primeras relaciones y los 6 primeros exámenes:

  1. Definiciones elementales de funciones (1).
  2. Definiciones elementales de funciones (2).
  3. Definiciones por comprensión (1).
  4. Definiciones por comprensión (2).
  5. Definiciones por comprensión (3): El cifrado César.
  6. Definiciones por recursión.
  7. Definiciones por recursión y por comprensión (1).
  8. Definiciones por recursión y por comprensión (2).
  9. Definiciones sobre cadenas, orden superior y plegado.
  10. Definiciones por plegado.
  11. Codificación y transmisión de mensajes.
  12. Resolución de problemas matemáticos.
  13. Demostración de propiedades por inducción.
  14. El 2011 y los números primos.
  15. Listas infinitas.
  16. Ejercicios de exámenes del curso 2010-11.
  17. Combinatoria.
  18. Tipos de datos algebraicos.
  19. Tipos de datos algebraicos: árboles binarios.
  20. Tipos de datos algebraicos: fórmulas proposicionales.
  21. Tipos de datos algebraicos: Modelización de juego de cartas.
  22. Cálculo numérico.
  23. Ecuación con factoriales.
  24. Aplicaciones de la programación funcional con listas infinitas.
  25. División y factorización de polinomios mediante la regla de Ruffini.
  26. Operaciones con el TAD de polinomios.
  27. Operaciones con vectores y matrices.
  28. Ejercicios complementarios.
  29. Relaciones binarias.
  30. Operaciones con conjuntos.
  31. Implementación del TAD de los grafos mediante listas.
  32. Problemas básicos con el TAD de los grafos.
  33. Enumeraciones de los números racionales.
  34. Exámenes:
    • Examen 1 (26 de Octubre de 2011).
    • Examen 2 (30 de Noviembre de 2011).
    • Examen 3 (25 de Enero de 2012).
    • Examen 4 (29 de Febrero de 2012).
    • Examen 5 (21 de Marzo de 2012).
    • Examen 6 (2 de Mayo de 2012).

El método de Pólya para resolver problemas

PorJosé A. Alonso

George Pólya presentó en su libro Cómo plantear y resolver problemas (en inglés, How to solve it) un método de 4 pasos para resolver problemas matemáticos. Dicho método fue adaptado para resolver problemas de programación, por Simon Thompson en How to program it.

En la siguientes secciones mostramos los 4 pasos de ambos métodos, junto con sus correspondientes preguntas.
Read More “El método de Pólya para resolver problemas”