Software Libre para la Enseñanza y el Aprendizaje de las Matemáticas (2010-11) Software Libre para la Enseñanza y el Aprendizaje de las Matemáticas (2010-11)

Enunciado:

A) Determina los extremos relativos de la función f(x)=x^2-4x+2. Dibuja su gráfica.

B) Hallar las ecuaciones de los dos rectas tangentes a la gráfica de f que pasan por el punto P(3,-5).

---

Solución:

A) Determina los extremos relativos de la función f(x)=x^2-4x+2. Dibuja su gráfica.

(%i58) f(x):=x^2-4*x+2;
df(x):=diff(f(x),x);
df(x);
(%o58) f(x):=x^2-4*x+2
(%o59) df(x):=diff(f(x),x)
(%o60) 2*x-4
(%i61) solve(df(x),x);
(%o61) [x=2]

Comprobamos el signo de la derivada segunda para saber si es máximo o mínimo

(%i62) df2(x):=diff(f(x),x,2);
df2(x);
(%o62) df2(x):=diff(f(x),x,2)
(%o63) 2
(%i68) wxplot2d([f(x)],[x,-2,6],[y,-4,4]);
plot2d: some values were clipped.
(%t68)  << Graphics >> 
(%o68)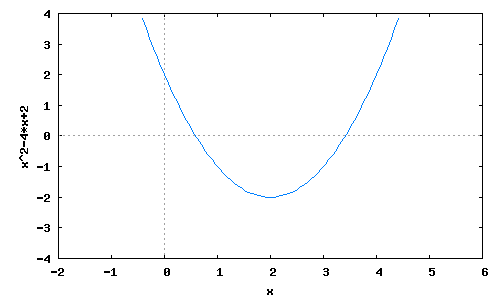 

B) Hallar las ecuaciones de los dos rectas tangentes a la gráfica de f que pasan por el punto P(3,-5).

(%i4) g(x):=taylor(f(x),x,a,1);
g(x);
(%o4) g(x):=taylor(f(x),x,a,1)
(%o5)/T/ 2-4*a+a^2+(2*a-4)*(x-a)+...

Defino la ecuación de la recta tangente a la función f(x) en función del punto (a,f(a)) en el que se calcula. Este punto es la incógnita que hay que calcular, para ello imponemos que la recta pase por P(3,-5).

(%i7) g(x):=2-4*a+a^2+(2*a-4)*(x-a);
(%o7) g(x):=2-4*a+a^2+(2*a-4)*(x-a)
(%i8) solve(g(3)=-5,a);
(%o8) [a=1,a=5]

Las dos soluciones son a=1 y a=5 para lo cual calculamos las rectas tangentes en esos puntos

(%i10) y1(x):=taylor(f(x),x,1,1);
y1(x);
(%o10) y1(x):=taylor(f(x),x,1,1)
(%o11)/T/ -1-2*(x-1)+...
(%i12) y2(x):=taylor(f(x),x,5,1);
y2(x);
(%o12) y2(x):=taylor(f(x),x,5,1)
(%o13)/T/ 7+6*(x-5)+...

Comprobamos el resultado dibujando tanto la función como las rectas tangentes.

(%i15) wxplot2d([f(x),y1(x),y2(x)],[x,-4,6],[y,-7,7]);
(%t15)  
(%o15)