Software Libre para la Enseñanza y el Aprendizaje de las Matemáticas (2010-11) Software Libre para la Enseñanza y el Aprendizaje de las Matemáticas (2010-11)

Enunciado:

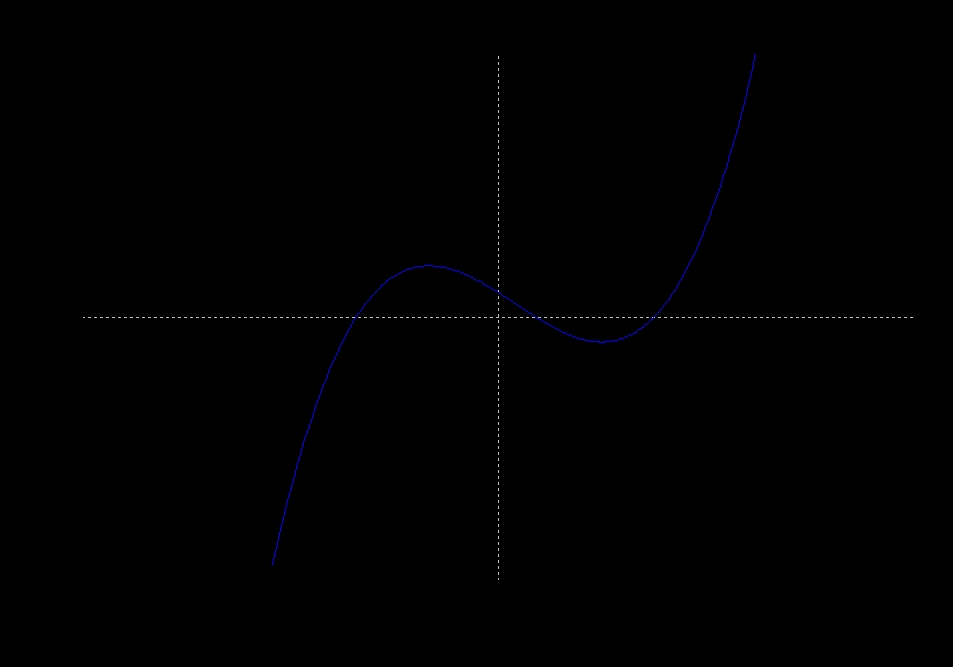
• Representar gráficamente la función f(x)=2*x^3-[(x^2)/2]-x+(5/27)

Solución:

• Definir la función

(%i1) f(x):=2*x^3-[(x^2)/2]-x+(5/27)
(%o1) f(x):=2*x^3-[x^2/2]-x+5/27

• Para poder representarla vamos a estudiar su derivada

(%i2) 'diff(f(x),x)=diff(f(x),x);
(%o2) 'diff([2*x^3-x^2/2-x+5/27],x,1)=[6*x^2-x-1]

• Igualando a cero resulta:(Resolver la ecuación (6*x^2-x-1=0))

(%i3) solve(6*x^2-x-1=0);
(%o3) [x=-1/3,x=1/2]

• Construimos una tabla para estudiar el signo de la derivada y conocer así donde crece y donde decrece y sus máximos y mínimos. Y sacamos que:

- Crece (- infinito, -1/3) - Decrece (-1/3,1/2) - Máximo (-1/3,7/18) - Mínimo (1/2,41/216)

• También es obvio que:

(%i4)limit(f(x),x,-inf);
(%o4)[-inf]

(%i5)limit(f(x),x,inf);
(%o5)[+inf]

• La gráfica resultante es:

plot2d(f(x),[x,-2,2],[y,-2,2])$
(%i6) wxplot2d(f(x),[x,-2,2],[y,-2,2])$