Diferencia entre revisiones de «Relación 4»
De Lógica informática (2014-15)
(Página creada con '=== Relación 4: Temas 1 y 2 === ---- '''Ejercicio 1.''' Juan está matriculado en tres asignaturas: Álgebra, Lógica y Dibujo. Juan comenta lo siguiente: <blockquote> Me gus...') |
|||
| (No se muestran 2 ediciones intermedias del mismo usuario) | |||
| Línea 10: | Línea 10: | ||
'''Solución:''' | '''Solución:''' | ||
| + | |||
| + | {A∨L∨D, A∧¬D→L, (D∧L)∨(¬D∧¬L), D→A} | ||
| + | |||
| + | Solo tiene un modelo: I(F1)=I(F2)=I(F3)=I(F4)=1 => Que le gusten las tres asignaturas | ||
| + | |||
---- | ---- | ||
| Línea 16: | Línea 21: | ||
'''Solución:''' | '''Solución:''' | ||
| + | |||
| + | Falso: ¬p ∧ p ⊧ p | ||
| + | |||
| + | F= ¬p ∧ p; esta fórmula, al ser una contradicción, no es satisfacible. | ||
| + | Pero {p}, que es consecuencia lógica de F, por ∧2, si es satisfacible. | ||
---- | ---- | ||
| Línea 23: | Línea 33: | ||
'''Solución:''' | '''Solución:''' | ||
| + | |||
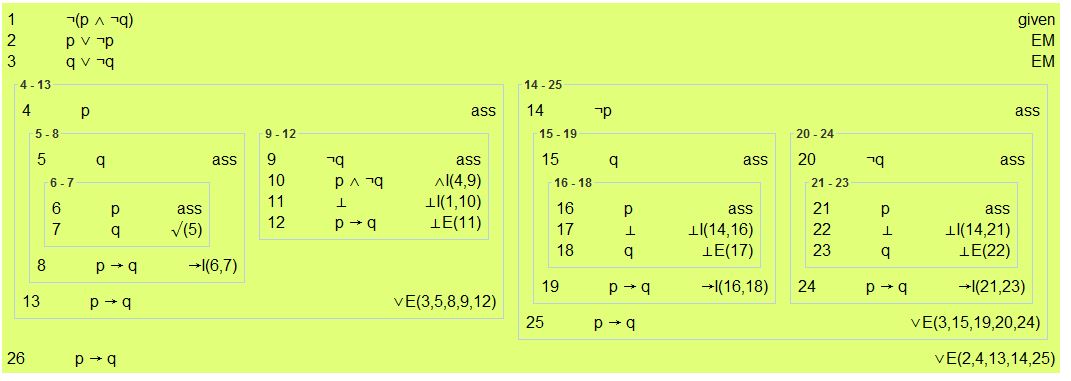
| + | [[Archivo:Ejercicio_3.JPG]] | ||
---- | ---- | ||
| Línea 31: | Línea 43: | ||
'''Solución:''' | '''Solución:''' | ||
| + | |||
| + | [[Archivo:Ejercicio_4.JPG]] | ||
---- | ---- | ||
| Línea 36: | Línea 50: | ||
: ⊧ (¬ q → ¬ p) ∨ (q → p) | : ⊧ (¬ q → ¬ p) ∨ (q → p) | ||
---- | ---- | ||
| + | |||
| + | '''Solución:''' | ||
| + | |||
| + | [[Archivo:Ejercicio_5.JPG]] | ||
Revisión actual del 12:07 18 oct 2014
Relación 4: Temas 1 y 2
Ejercicio 1. Juan está matriculado en tres asignaturas: Álgebra, Lógica y Dibujo. Juan comenta lo siguiente:
Me gusta al menos una de las tres asignaturas. Si me gustase el Álgebra pero no el Dibujo, me gustaría la Lógica. O me gusta el Dibujo y la Lógica, o bien ninguna de las dos. Si me gustase el Dibujo, entonces me gustaría el Álgebra.
Formalizar los comentarios de Juan, usando la inicial de cada asignatura para representar que a Juan le gusta dicha asignatura. Decidir si los comentarios son consistentes y, en su caso, calcular sus modelos. ¿Qué asignaturas le gustan a Juan?
Solución:
{A∨L∨D, A∧¬D→L, (D∧L)∨(¬D∧¬L), D→A}
Solo tiene un modelo: I(F1)=I(F2)=I(F3)=I(F4)=1 => Que le gusten las tres asignaturas
Ejercicio 2. Demostrar o refutar la siguiente afirmación: "F es satisfacible si y sólo si toda consecuencia lógica de F es satisfacible."
Solución:
Falso: ¬p ∧ p ⊧ p
F= ¬p ∧ p; esta fórmula, al ser una contradicción, no es satisfacible. Pero {p}, que es consecuencia lógica de F, por ∧2, si es satisfacible.
Ejercicio 3. Demostrar mediante deducción natural:
- ¬(p ∧ ¬ q) ⊧ p → q
Solución:
Ejercicio 4. Demostrar mediante deducción natural:
- (p ∨ q) ∧ (q → r) ⊧ p ∨ r.
Solución:
Ejercicio 5. Demostrar mediante deducción natural:
- ⊧ (¬ q → ¬ p) ∨ (q → p)
Solución: