Diferencia entre revisiones de «Relación 9»
De Lógica informática (2014-15)
(Página creada con '=== Relación 9: Temas 1 a 7 === ---- '''Ejercicio 1.''' Formalizar el siguiente argumento <blockquote> Todos los participantes son vencedores. Hay como máximo un vencedor. Ha...') |
(→Relación 9: Temas 1 a 7) |
||
| (No se muestra una edición intermedia del mismo usuario) | |||
| Línea 10: | Línea 10: | ||
---- | ---- | ||
| − | '''Solución:''' | + | '''Solución:''' |
| + | |||
| + | [[Archivo:Ejercicio_1.PNG]] | ||
---- | ---- | ||
| Línea 20: | Línea 22: | ||
'''Solución:''' | '''Solución:''' | ||
| + | |||
| + | [[Archivo:Ejercicio_2.PNG]] | ||
---- | ---- | ||
| Línea 27: | Línea 31: | ||
'''Solución:''' | '''Solución:''' | ||
| + | |||
| + | [[Archivo:Ejercicio_3.PNG]] | ||
---- | ---- | ||
| Línea 35: | Línea 41: | ||
'''Solución:''' | '''Solución:''' | ||
| + | |||
| + | [[Archivo:Ejercicio_4a.PNG]] | ||
| + | [[Archivo:Ejercicio_4b.PNG]] | ||
---- | ---- | ||
| Línea 42: | Línea 51: | ||
'''Solución:''' | '''Solución:''' | ||
| + | |||
| + | [[Archivo:Ejercicio_5.PNG]] | ||
Revisión actual del 16:43 3 dic 2014
Relación 9: Temas 1 a 7
Ejercicio 1. Formalizar el siguiente argumento
Todos los participantes son vencedores. Hay como máximo un vencedor. Hay como máximo un participante. Por lo tanto, hay exactamente un participante.
Nota: Comprobar la formalización con APLI2.
Solución:
Ejercicio 2. Demostrar o refutar la siguiente proposición
Si la fórmula F se puede demostrar por deducción natural a partir del conjunto de fórmulas S y también se puede demostrar a partir del conjunto de fórmulas T, entonces F se puede demostrar por deducción natural a partir de la intersección de S y T.
Solución:
Ejercicio 3. Demostrar por deducción natural
- ((p → q ∧ ¬ r) → p) → p
Solución:
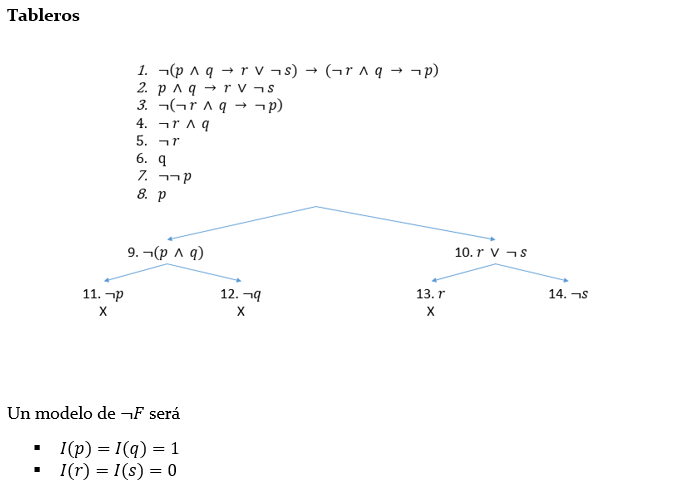
Ejercicio 4. Decidir, mediante tableros semánticos, si la fórmula
- F : (p ∧ q → r ∨ ¬ s) → (¬ r ∧ q → ¬ p)
es una tautología. Si no lo es, calcular a partir del tablero, un modelo de ¬F, una forma normal conjuntiva de F y una forma clausal de F.
Solución:
Ejercicio 5. Probar por resolución proposicional que
- {p ∨ q ↔ ¬r, ¬p → s, ¬t → q, s ∧ t → u } ⊢ r → u.
Solución: