Diferencia entre revisiones de «Relación 5»
De Lógica informática (2014-15)
| (No se muestran 4 ediciones intermedias del mismo usuario) | |||
| Línea 39: | Línea 39: | ||
'''Solución:''' | '''Solución:''' | ||
| − | + | Si las premisas son (¬C∧¬A)⇒B, ¬A⇒¬B y esto confirma que C∨A según el tío Jaime. Podemos concluir que es cierto por tablero semántico | |
| + | [[Archivo:Tablero semantico opcion tio jaime.JPEG]] | ||
| + | |||
---- | ---- | ||
'''Ejercicio 3.''' Probar que la fórmula | '''Ejercicio 3.''' Probar que la fórmula | ||
| Línea 46: | Línea 48: | ||
---- | ---- | ||
| − | '''Solución: [[Archivo:TABLERO SEMANTICO.JPEG]]''' | + | '''Solución: [[Archivo:TABLERO SEMANTICO.JPEG]] |
| + | [[Archivo:DEDUCCION NATURAL.JPEG]]''' | ||
---- | ---- | ||
| Línea 56: | Línea 59: | ||
'''Solución:''' | '''Solución:''' | ||
| + | Analizando el ejemplo de la transparencia 22 del tema 3, se comprueba que el número de nodos es igual usando indistintamente primero fórmulas alfa o beta. Por lo cual podemos decir que la afirmación del enunciado es falsa. | ||
---- | ---- | ||
| Línea 63: | Línea 67: | ||
---- | ---- | ||
| − | '''Solución:''' | + | '''Solución:[[Archivo:DEDUCCION NATURAL1.JPEG]]''' |
| + | |||
| + | [[Archivo:FNC Relacion 5.JPEG]] | ||
Revisión actual del 20:00 2 nov 2014
Relación 5: Temas 1 a 4
Ejercicio 1. Demostrar o refutar las siguientes proposiciones:
- F ∧ G es satisfacible syss F es satisfacible y G es satisfacible.
- F ∨ G es satisfacible syss F es satisfacible o G es satisfacible.
Solución:
Solucion 1:
- 1.F ∧ G es satisfacible syss F es satisfacible y G es satisfacible.
Para que F ∧ G sea satisfacible debe valer 1 y esto solo ocurre cuando ambas funciones valen 1, por lo que F y G tienen que ser ambas satisfacibles para que la expresión F ∧ G sea satisfacible .
- 2.F ∨ G es satisfacible syss F es satisfacible o G es satisfacible.
Para que F ∨ G sea satisfacible debe valer 1 y en este caso la expresión valdrá 1 excepto para el caso en el que tanto F como G valen 0. Entonces F ∨ G es satisfacible siempre que solo una de las funciones F o G sea satisfacible.
Solucion 2 :
1 es falso
F ∧ G ,supongamos p∧¬p,en este ejemplo ambas funciones son satisfacibles pero p∧¬p no lo es.
Ejercicio 2. En un texto de Lewis Carroll, el tío Jorge y el tío Jaime discuten acerca de la barbería del pueblo, atendida por tres barberos: Alberto, Benito y Carlos. Los dos tíos aceptan las siguientes premisas:
- Si Carlos no está en la barbería, entonces ocurrirá que si tampoco está Alberto, Benito tendrá que estar para atender el establecimiento.
- Si Alberto no está, tampoco estará Benito.
El tío Jorge concluye de todo esto que Carlos no puede estar ausente, mientras que el tío Jaime afirma que sólo puede concluirse que Carlos y Alberto no pueden estar ausentes a la vez. Decidir con el método de los tableros semánticos cuál de los dos tiene razón y demostrarlo por deducción natural.
Solución:
Si las premisas son (¬C∧¬A)⇒B, ¬A⇒¬B y esto confirma que C∨A según el tío Jaime. Podemos concluir que es cierto por tablero semántico

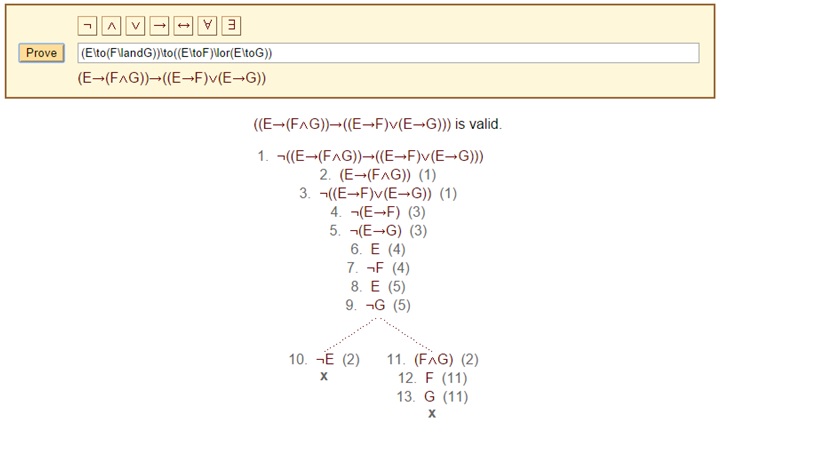
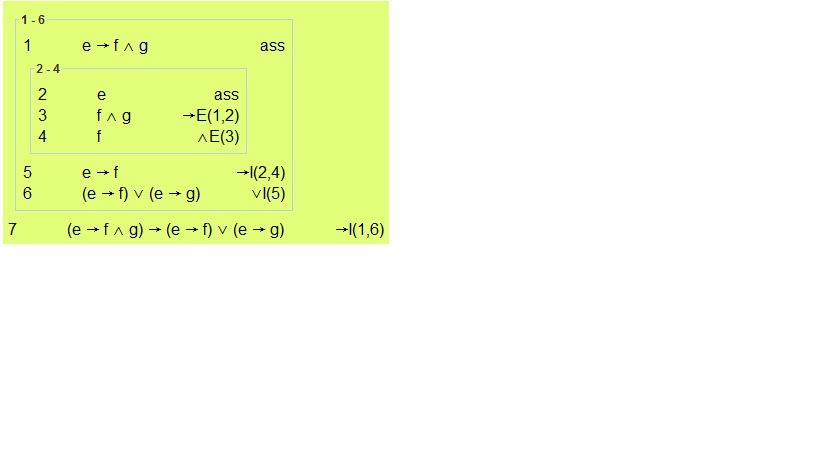
Ejercicio 3. Probar que la fórmula
- (E → (F ∧ G)) → (E → F) ∨ (E → G)
es una tautología por tableros semánticos y por deducción natural.
Ejercicio 4. Demostrar o refutar la siguiente proposición:
Si S es un conjunto inconsistente de fórmulas, entonces el tablero semántico cerrado de S obtenido aplicando las reglas α antes que las reglas β tiene menos nodos que el tablero semántico cerrado de S obtenido aplicando las reglas β antes que las reglas α.
Solución: Analizando el ejemplo de la transparencia 22 del tema 3, se comprueba que el número de nodos es igual usando indistintamente primero fórmulas alfa o beta. Por lo cual podemos decir que la afirmación del enunciado es falsa.
Ejercicio 5. Probar, mediante forma normal conjuntiva y mediante deducción natural, que la fórmula
- (p → ¬q ∧ r) → (p → (q → r))
es una tautología