Diferencia entre revisiones de «Ejercicios 2: Funciones de una variable»
De Software Libre para la Enseñanza y el Aprendizaje de las Matemáticas (2010-11)
(→Ejercicio 3.4) |
(→Ejercicio 3.5) |
||
| Línea 145: | Línea 145: | ||
'''Solución:''' | '''Solución:''' | ||
| + | --> plot2d([T3(x),T4(x), T5(x)], [x,-1,1])$ | ||
| + | (%i15) wxplot2d([T3(x),T4(x), T5(x)], [x,-1,1])$ | ||
| + | (%t15)(sale el dibujo de la gráfica)[[Archivo:image.png]] | ||
Revisión del 09:12 6 abr 2011
Funciones a utilizar: if...then...else, assume, limit, forget, plot2d, diff, define, solve, trigexpand, trigsimp y subst.
Ejercicio 1
Sean <math>a</math> y <math>b</math> dos números reales. Se considera la función <math>f</math> definida sobre los números reales por
- <math>
f(x)=\left\{ \begin{array}{lll}
\dfrac{e^x-1}{x} &\mbox{si} & x>0\\
a\,x+b &\mbox{si} & x\leq 0
\end{array} \right. </math>
Ejercicio 1.1
Definir la función <math>f</math> usando el condicional if ... then ... else.
Solución:
(%i1)d(x):=if x>0 then (e^x-1)/x else ax+b;
Ejercicio 1.2
limit no puede evaluar expresiones del tipo if...then. Por ello, para determinar el límite de <math>f</math> en cero por la derecha se necesita precisar en qué intervalo se encuentra <math>x</math>. Esto puede hacerse con la función assume.
Escribir la expresión assume(x>0), después calcular el límite de <math>f</math> en cero por la derecha. Se puede eliminar la hipótesis sobre <math>x</math> con forget(x>0).
Solución:
Ejercicio 1.3
Deducir el valor de <math>b</math> para el que <math>f</math> es continua en <math>\mathbb{R}</math>.
Solución:
f(x) se trata de una función a trozos tal que:
1. Para x > 0, f(x) es un cociente entre funciones continuas en R, por tanto, podrá presentar problemas de discontinuidad en los puntos en los que su denominador se anula, eso sólo ocurre para x=0, pero en ese punto, f(x) presenta otro comportamiento.
2. Para x<= 0, f(x) es una función lineal, y por tanto, continua en todo R.
Por consiguiente, el único punto en el que la función a trozos puede presentar problemas es donde cambia de criterio, en x = 0.
Para que f(x) sea continua en x = 0, deben ser iguales los límites laterales de la función en dicho punto:
solve(limit((exp(x)-1)/x,x,0)=limit(a*x+b,x,0));
Devolviéndonos que b = 1.
Ejercicio 1.4
Calcular la derivada de <math>f</math> en cero por la derecha.
Solución:
Ejercicio 1.5
Calcular el valor de <math>a</math> para el que <math>f</math> es derivable en cero.
Solución:
Ejercicio 2
Sea <math>g</math> la función real definida por <math>g(x) = 2x-\sqrt{1+x^2}</math>
(%i1)g(x):= 2*x-sqrt(1+x^2)$
Ejercicio 2.1
Calcular los límites de <math>g</math> en más y menos infinito.
Solución:
(%01) g(x):= 2*x-sqrt(1+x^2)$ (%02) limit(g(x),x,inf); (%02) inf (%03) limit(g(x),x,-inf); (%03) -inf
<math> inf, -inf</math>
Ejercicio 2.2
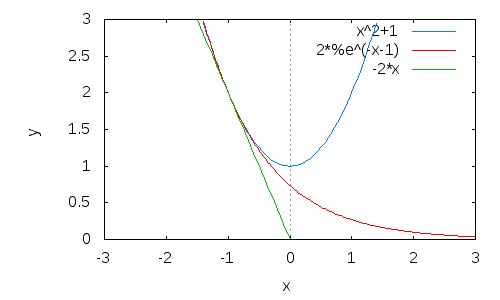
Dibujar la gráfica de la función <math>g</math>.
Solución:
(%o4) wxplot2d(g(x), [x,-2,2],[y,-3,3]);[gnuplot_preamble, "set grid "])$ plot2d: some values were clipped. (%t05) << Graphics >>
No sale la gráfica.
Ejercicio 2.3
Calcular <math>g'(x)</math>.
Solución:
(%i1) g(x):= 2*x-sqrt(1+x^2); (%i2)diff(g(x),x); (%02)2-x/sqrt(x^2+1);
Ejercicio 2.4
Resolver la ecuación <math>g(x)=0</math>.
Solución:
(%i1) g(x):= 2*x-sqrt(1+x^2); (%i2) g(0); (%02) -1
Ejercicio 2.5
Determinar los intervalos de crecimiento de <math>g</math>.
Solución:
Ejercicio 2.6
Calcular las ecuaciones reducidas de las asíntotas de <math>g</math>.
Solución:
Ejercicio 3
Ejercicio 3.1
Desarrollar <math>cos(3t)</math> en función de <math>cos(t)</math>.
Solución:
(%i1) trigexpand(cos(3*t)); (%o1) cos(t)^3-3*cos(t)*sin(t)^2 (%i2) trigsimp(%); (%o2) 4*cos(t)^3-3*cos(t)
Ejercicio 3.2
Desarrollar <math>cos(4t)</math> en función de <math>cos(t)</math>
Solución:
(%i3) trigexpand(cos(4*t)); (%o3) sin(t)^4-6*cos(t)^2*sin(t)^2+cos(t)^4 (%i4) trigsimp(%); (%o4) 8*cos(t)^4-8*cos(t)^2+1
Ejercicio 3.3
Desarrollar <math>cos(5t)</math> en función de <math>cos(t)</math>.
Solución:
(%i5) trigexpand(cos(5*t)); (%o5) 5*cos(t)*sin(t)^4-10*cos(t)^3*sin(t)^2+cos(t)^5 (%i6) trigsimp(%); (%o6) 16*cos(t)^5-20*cos(t)^3+5*cos(t)
Ejercicio 3.4
Determinar los polinomios <math>T_n</math> de la variable <math>x</math> tales que para todo <math>t \in \mathbb{R}</math>, <math>cos(nt) = T_n(cos\ t)</math> para <math>n \in \{3,4,5\}</math>.
Solución:
(%i12) T3(x) := 4*x^3-3*x; (%o12) T3(x):=4*x^3-3*x (%i13) T4(x) := 8*x^4-8*x^2+1; (%o13) T4(x):=8*x^4-8*x^2+1 (%i14) T5(x) := 16*x^5-20*x^3+5*x; (%o14) T5(x):=16*x^5-20*x^3+5*x
Ejercicio 3.5
Representar las funciones <math>T_3</math>, <math>T_4</math> y <math>T_5</math> en la misma gráfica.
Solución:
--> plot2d([T3(x),T4(x), T5(x)], [x,-1,1])$ (%i15) wxplot2d([T3(x),T4(x), T5(x)], [x,-1,1])$ (%t15)(sale el dibujo de la gráfica)