2010 Ejercicios 4: Sucesiones y recursión

Ejercicio 1

Ejercicio 1.1.

La sucesión de Fibonacci está definida como

  F[0]   = 0,
  F[1]   = 1, 
  F[n+2] = F[n+1]+F[n].

Definir f[n] como la sucesión de Fibonacci.

Solución:

 (%i1)f[0]:0$
      f[1]:1$
      f[n]:=f[n-1]+f[n-2]$

Ejercicio 1.2.

Definir la lista l1 cuyos elementos son los 20 primeros términos de la sucesión de Fibonacci.

Solución:

 (%i2)l1: makelist(f[n],n, 0,19);
 (%02)[0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181]

Ejercicio 1.3.

Calcular el término que ocupa la posición 20 en la sucesión de Fibonacci.

Solución:

 (%i3)f[19];
 (%03)4181

Ejercicio 1.4.

Calcular el término de posición 20 de la sucesión de Fibonacci de forma iterativa, usando sólo dos variables: a y b.

Solución:

Ejercicio 1.5.

Definir la sucesión g, que calcule el término n-ésimo de la sucesión de Fibonacci de forma iterativa, usando sólo dos variables: a y b. Usando la función g, calcular el término de posición 20 de la sucesión de Fibonacci.

Solución:

Ejercicio 1.6.

Comprobar si se puede obtener el término 800 de la sucesión de Fibonacci mediante alguna de las dos funciones f ó g.

Solución:

Ejercicio 2

Ejercicio 2.1.

Definir s[n] como la suma de los n primeros términos de la sucesión (-1)^(k+1)/k!

Solución:

  (%i1)s[n]:=sum((-1)^(k+1)/k!,k,0,n);

Ejercicio 2.2.

Calcular los valores exactos de s[1], s[2], s[5] y s[9].

Solución:

 (%i2)s[1];
 (%02)0

 (%i3)s[2];
 (%03)-1/2

 (%i4)s[5];
 (%04)-11/30

 (%i5)s[9];
 (%05)-16687/45360

Ejercicio 2.3.

Calcular los valores decimales aproximados de s[20] y s[50].

Solución:

 (%i6)float(s[20]);
 (%06)-0.36787944117144

 (%i7)float(s[50]);
 (%07)-0.36787944117144

Ejercicio 2.4.

Cargar el paquete simplify_sum y calcular la suma de la serie s[n].

Solución:

 (%i8)load(simplify_sum)$ sum((-1)^(k+1)/k!,k,0,inf) $ simplify_sum(%);
 (%08)-%e^(-1)

Ejercicio 3

Un banco presta un capital K al t por ciento aunual, que se reembolsa en N años, con anualidades x constante. Sea c[0]=K y sea c[n] el capital pendiente de pagar después de la n-ésima anualidad. Entonces,

c[n+1] = (1+t)*c[n]-x

Ejercicio 3.1.

Expresar c[n] de manera explícita en función de n, K, t y x.

Solución:

(%i1) load(solve_rec)$
(%i2) solve_rec(c[n+1] = (1+t)*c[n]-x,c[n],c[0]=K);
(%o2) c[n]=(t+1)^n*K-((t+1)^n*x)/t+x/t
(%i3) ratsimp(%);
(%o3) c[n]=(t*(t+1)^n*K+(1-(t+1)^n)*x)/t

Ejercicio 3.2.

Se sabe que c[N]=0. Deducir el valor de x en función de K, t y N.

Solución:

(%i1) f(x):=(t*(t+1)^N*K+(1-(t+1)^N)*x)/t;
(%i2) linsolve([(t*(t+1)^N*K+(1-(t+1)^N)*x)/t], [x]);
(%o2) [x=(t*(t+1)^N*K)/((t+1)^N-1)]

Ejercicio 3.3.

Calcular el importe de una anualidad, cuando K = 100000, t = 5,5% y N = 15.

(%i1) K: 100000$
(%i2) t:5.5$
(%i3) N:15$
(%i4) linsolve([(t*(t+1)^N*K+(1-(t+1)^N)*x)/t], [x]);
 rat: replaced 0.18181818181818 by 2/11 = 0.18181818181818
 rat: replaced 8.5913821892547354E+17 by 859138218925473536/1 = 8.5913821892547354E+17
 rat: replaced -1.562069488954407E+12 by -1562069488954/1 = -1.562069488954E+12
(%o4) [x=429569109462736768/781034744477]
(%i5) float(%)
(%o5) [x=550000.0000004952]

Ejercicio 4

Ejercicio 4.1.

Definir la función f(x) = x/(3-2x).

Solución:

(%i1) f(x):=x/(3-2*x)$

Ejercicio 4.2.

Definir la sucesión u[n] tal que

  u[0]   = 2
  u[n+1] = f(u[n]) 

Solución:

(%i1) u[0] : 2$
      u[n] := f(u[n-1])$

Ejercicio 4.3.

Calcular u[1], u[2] y u[9].

Solución:

(%i1) u[1];
(%o1) -2
(%i2) u[2];
(%o2) -2/7
(%i3) u[9];
(%o3) -2/19681

Ejercicio 4.4.

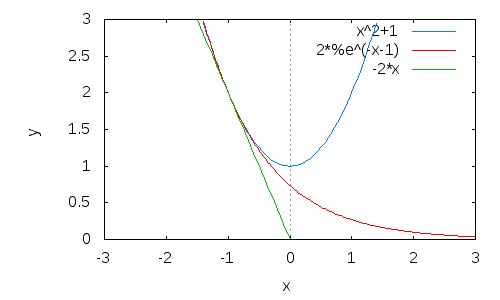
Dibujar, en la misma gráfica, la función f, la recta de ecuación y=x y los puntos de coordenada (u[k],f(u[k])) para 0<=k<=15.

Solución:

(%i1) L1:makelist([u[k],f(u[k])],k,0,15);
(%i2) wxplot2d([f(x),x,[discrete,L1]], [x,-2,2], [y,-2,2],
      [style, [lines,2,1], [lines,1,2], [linespoints,1,2,3,1]],
      [gnuplot_preamble, "set grid"],
      [legend, "y=f(x)", "y=x", "suite u"])$

Ejercicio 4.5.

Conjeturar la monotonía de la sucesión u[n] y su limite.

Solución:

Ejercicio 4.6.

Resolver la ecuación f(x)=x. Llamar a las raices a y b.

Solución:

 (%i1)a: first(solve([f(x)=x], [x]));
 (%01)x=0
 (%i2)b: second(solve([f(x)=x], [x]));
 (%02)x=1
 (%i3)a;b;
 (%03) x=0
       x=1

Ejercicio 4.7.

Definir la sucesión w[n] = (u[n]-a)/(u[n]-b)

Solución:

(%i8) w[n]:= (u[n]-a)/(u[n]-b) ;

Ejercicio 4.8.

Calcular los 10 primeros términos de la sucesión w[n].

Solución:

Ejercicio 4.9.

Comprobar que w[n] es una progresión geométrica y calcular su razón.

Solución:

Ejercicio 4.10.

Deducir la expresión de u[n] en función de n.

Solución: