Diferencia entre revisiones de «Ejercicios libres»
De Software Libre para la Enseñanza y el Aprendizaje de las Matemáticas (2010-11)
| Línea 17: | Línea 17: | ||
'''Solucion:''' | '''Solucion:''' | ||
| − | 1.- Definimos: | + | '''1.-''' Definimos: |
| + | |||
( %i1) g(x):=1/(1+x^2); | ( %i1) g(x):=1/(1+x^2); | ||
( %o1) | ( %o1) | ||
| − | g (x) :=1/1 + x2 | + | g (x) :=1/1 + x2 |
( %i2) h(x):=1+log(x); | ( %i2) h(x):=1+log(x); | ||
| Línea 31: | Línea 32: | ||
( %i3) solve(1+x^2=0); | ( %i3) solve(1+x^2=0); | ||
| − | |||
( %o3) | ( %o3) | ||
[x = -i; x = i] | [x = -i; x = i] | ||
| Línea 58: | Línea 58: | ||
El único punto de corte es x = 1/e . En cuanto a posibles puntos de corte con el eje | El único punto de corte es x = 1/e . En cuanto a posibles puntos de corte con el eje | ||
vertical, cuando x = 0 nuestra función toma el valor f(0) = g(0) = 1: | vertical, cuando x = 0 nuestra función toma el valor f(0) = g(0) = 1: | ||
| + | |||
( %i9) g(0); | ( %i9) g(0); | ||
( %o9) | ( %o9) | ||
1 | 1 | ||
| + | |||
En definitiva: | En definitiva: | ||
Los puntos de corte de f(x) son (0; 1) y ( 1/e ; 0). | Los puntos de corte de f(x) son (0; 1) y ( 1/e ; 0). | ||
| Línea 67: | Línea 69: | ||
es siempre distinto de cero. La función h(x) tendría una asíntota vertical | es siempre distinto de cero. La función h(x) tendría una asíntota vertical | ||
en x = 0, debido al logaritmo: | en x = 0, debido al logaritmo: | ||
| + | |||
( %i10) limit(h(x),x,0,plus); | ( %i10) limit(h(x),x,0,plus); | ||
( %o10) | ( %o10) | ||
-infinito | -infinito | ||
| + | |||
Pero esto no afecta a f(x) ya que, en los alrededores de x = 0, esta función no toma los | Pero esto no afecta a f(x) ya que, en los alrededores de x = 0, esta función no toma los | ||
valores de h(x), sino de g(x). Por lo tanto, f no tiene ninguna asíntota vertical. | valores de h(x), sino de g(x). Por lo tanto, f no tiene ninguna asíntota vertical. | ||
Con respecto a asíntotas horizontales, tendremos que estudiar límites de f(x) | Con respecto a asíntotas horizontales, tendremos que estudiar límites de f(x) | ||
| − | cuando x -> -infinito (en cuyo caso f = g) y cuando x -> +infinito (en cuyo caso f = h) | + | cuando x -> -infinito (en cuyo caso f = g) y cuando x -> +infinito (en cuyo caso f = h) |
| + | |||
( %i11) limit(g(x),x,minf); | ( %i11) limit(g(x),x,minf); | ||
( %o11) | ( %o11) | ||
0 | 0 | ||
| + | |||
( %i12) limit(h(x),x,inf); | ( %i12) limit(h(x),x,inf); | ||
( %o12) | ( %o12) | ||
infinito | infinito | ||
| + | |||
Por lo tanto, podemos concluir que: | Por lo tanto, podemos concluir que: | ||
f(x) no tiene ninguna asíntota vertical y tiene una asíntota horizontal (la | f(x) no tiene ninguna asíntota vertical y tiene una asíntota horizontal (la | ||
| Línea 85: | Línea 92: | ||
| − | 2.- Las funciones g(x) y h(x) son continuas dentro de sus respectivos dominios, por | + | '''2.-''' Las funciones g(x) y h(x) son continuas dentro de sus respectivos dominios, por |
lo tanto f es continua salvo, eventualmente, en x = 1, el punto que divide las regiones | lo tanto f es continua salvo, eventualmente, en x = 1, el punto que divide las regiones | ||
donde f toma los valores de g y de h. Pero los límites laterales de f en este | donde f toma los valores de g y de h. Pero los límites laterales de f en este | ||
| − | punto son distintos, pues | + | punto son distintos, pues: |
| + | |||
( %i13) limit(g(x),x,1,minus); | ( %i13) limit(g(x),x,1,minus); | ||
( %o13) | ( %o13) | ||
1/2 | 1/2 | ||
| + | |||
( %i14) limit(h(x),x,1,plus); | ( %i14) limit(h(x),x,1,plus); | ||
( %o14) | ( %o14) | ||
| Línea 99: | Línea 108: | ||
Además, f no es derivable en x = 1 (por no ser continua) pero sí en el resto de | Además, f no es derivable en x = 1 (por no ser continua) pero sí en el resto de | ||
R (pues tanto g como h lo son para valores de x que estén dentro de sus respectivos | R (pues tanto g como h lo son para valores de x que estén dentro de sus respectivos | ||
| − | dominios). Puesto que | + | dominios). Puesto que: |
| + | |||
( %i15) diff(g(x),x); | ( %i15) diff(g(x),x); | ||
( %o15) | ( %o15) | ||
| Línea 107: | Línea 117: | ||
( %o16) | ( %o16) | ||
1/x | 1/x | ||
| + | |||
| + | '''Representacion grafica:''' | ||
| + | |||
| + | Para representar la gráfica de f, podemos definir: | ||
| + | |||
| + | ( %i33) f(x):= if(x<1) then g(x) else h(x); | ||
| + | ( %o33) | ||
| + | f (x) := if x < 1 then g (x) else h (x) | ||
| + | |||
| + | El problema es que Maxima no está preparado para representar directamente este tipo | ||
| + | de funciones, siendo necesario encapsular f(x) en una expresión de la forma “’(f(x))”. | ||
| + | ( %i34) plot2d(f(x),[x,-5,5]); | ||
| + | Maxima was unable to evaluate the predicate: | ||
| + | ** error while printing error message ** | ||
| + | Maxima was unable to evaluate the predicate:~%~M | ||
| + | #0: f(x=x) | ||
| + | - an error. Quitting. To debug this try debugmode(true); | ||
| + | |||
| + | ( %i35) plot2d(’(f(x)),[x,-5,5], [gnuplot_preamble, "set zeroaxis"], | ||
| + | [gnuplot_term, ps], [gnuplot_out_file, "grafica.eps"]); | ||
| + | ( %o35) | ||
| + | |||
| + | [[Archivo:Ejemplo.jpg]] | ||
Revisión del 18:24 12 may 2010
En esta sección se encuentran ejercicios libremente enunciado por los alumnos y resueltos con los sistemas de software libre.
Autor: Jose David Cruz Margarin Problema:
Dada la función f(x):
1/1+x2 si x <= 1 1 + ln x si x > 1
1. Estudiar su dominio, puntos de corte y asíntotas.
2. Analizar su continuidad y derivabilidad.
Solucion:
1.- Definimos:
( %i1) g(x):=1/(1+x^2); ( %o1)
g (x) :=1/1 + x2
( %i2) h(x):=1+log(x); ( %o2)
h (x) := 1 + log x
El dominio de g es todo R pues, evidentemente, 1 + x2 6= 0 8x 2 R. Pero, por si hubiera alguna duda, el alumno podría utilizar Maxima para comprobar que no existe ninguna solución real (todas sus soluciones son imaginarios puros):
( %i3) solve(1+x^2=0); ( %o3)
[x = -i; x = i]
( %i4) solve(1+x^2=0); ( %o4)
[x = -i; x = i]
Maxima es incluso capaz de asegurarnos que 1+x2 es estrictamente positivo (independientemente del valor de x) si utilizamos la función is:
( %i5) is(1+x^2>0); ( %o5)
true
Para estudiar los puntos de corte con el eje de las abscisas, planteamos
( %i7) solve(g(x)=0,x); ( %o7)
[]
( %i8) solve(h(x)=0,x); ( %o8)
x = e-1
El único punto de corte es x = 1/e . En cuanto a posibles puntos de corte con el eje vertical, cuando x = 0 nuestra función toma el valor f(0) = g(0) = 1:
( %i9) g(0); ( %o9)
1
En definitiva: Los puntos de corte de f(x) son (0; 1) y ( 1/e ; 0).
En nuestro caso, la función g(x) no tiene ninguna asíntota vertical, porque su denominador es siempre distinto de cero. La función h(x) tendría una asíntota vertical en x = 0, debido al logaritmo:
( %i10) limit(h(x),x,0,plus); ( %o10)
-infinito
Pero esto no afecta a f(x) ya que, en los alrededores de x = 0, esta función no toma los valores de h(x), sino de g(x). Por lo tanto, f no tiene ninguna asíntota vertical. Con respecto a asíntotas horizontales, tendremos que estudiar límites de f(x) cuando x -> -infinito (en cuyo caso f = g) y cuando x -> +infinito (en cuyo caso f = h)
( %i11) limit(g(x),x,minf); ( %o11)
0
( %i12) limit(h(x),x,inf); ( %o12)
infinito
Por lo tanto, podemos concluir que: f(x) no tiene ninguna asíntota vertical y tiene una asíntota horizontal (la recta y = 0) cuando x -> -infinito.
2.- Las funciones g(x) y h(x) son continuas dentro de sus respectivos dominios, por
lo tanto f es continua salvo, eventualmente, en x = 1, el punto que divide las regiones
donde f toma los valores de g y de h. Pero los límites laterales de f en este
punto son distintos, pues:
( %i13) limit(g(x),x,1,minus); ( %o13)
1/2
( %i14) limit(h(x),x,1,plus); ( %o14)
1
en consecuencia, f no es continua en x = 1 (tendrá una discontinuidad de salto). Además, f no es derivable en x = 1 (por no ser continua) pero sí en el resto de R (pues tanto g como h lo son para valores de x que estén dentro de sus respectivos dominios). Puesto que:
( %i15) diff(g(x),x); ( %o15)
- 2x/(x2 + 1)2
( %i16) diff(h(x),x); ( %o16)
1/x
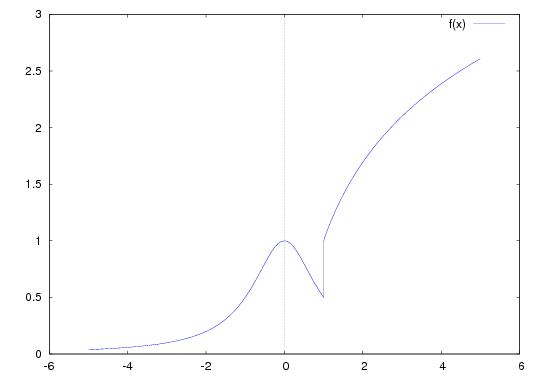
Representacion grafica:
Para representar la gráfica de f, podemos definir:
( %i33) f(x):= if(x<1) then g(x) else h(x); ( %o33)
f (x) := if x < 1 then g (x) else h (x)
El problema es que Maxima no está preparado para representar directamente este tipo de funciones, siendo necesario encapsular f(x) en una expresión de la forma “’(f(x))”. ( %i34) plot2d(f(x),[x,-5,5]); Maxima was unable to evaluate the predicate:
- error while printing error message **
Maxima was unable to evaluate the predicate:~%~M
- 0: f(x=x)
- an error. Quitting. To debug this try debugmode(true);
( %i35) plot2d(’(f(x)),[x,-5,5], [gnuplot_preamble, "set zeroaxis"], [gnuplot_term, ps], [gnuplot_out_file, "grafica.eps"]); ( %o35)