|
|
| Línea 3: |
Línea 3: |
| | Autor: Jose David Cruz Margarin | | Autor: Jose David Cruz Margarin |
| | | | |
| − | '''Problema:
| + | Problema: |
| − | Sea f(x)=(x^2-9)/x'''
| |
| | | | |
| − | 1.- Halla los puntos de corte de f(x) con los ejes de coordenadas.
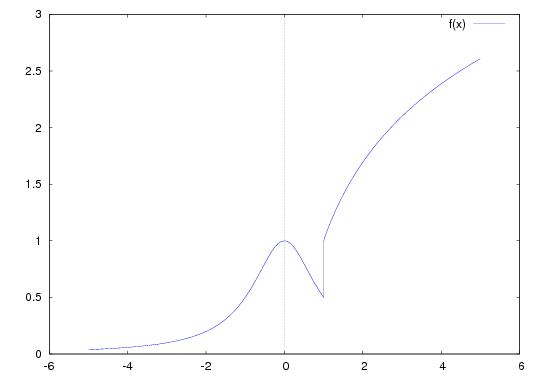
| + | Dada la función |
| | + | f(x) = 1/1+x2 si x <= 1 |
| | + | 1 + ln x si x > 1 |
| | | | |
| − | 2.- Presenta una lista con los valores de f(n); n = 100; 200; 300; : : : 1500. ¿Cuál piensas que es el límite de f(x) en +1? Confírmalo con wxMaxima. | + | 1. Estudiar su dominio, puntos de corte y asíntotas. |
| | + | 2. Analizar su continuidad y su derivabilidad, calcular su función derivada primera. |
| | + | 3. Determinar sus intervalos de crecimiento y decrecimiento, así como sus máximos |
| | + | y mínimos relativos. |
| | + | 4. Representar su gráfica. |
| | | | |
| − | 3.- Estudia las asíntotas verticales, horizontales y oblicuas de f(x).
| + | [[Archivo:Ejemplo.jpg]] |
| − | | |
| − | 4.- Representa de forma conjunta la gráfica de f(x) y de la recta y = x.
| |
| − | | |
| − | 5.- Halla la función derivada de f(x) y la recta tangente a f(x) en el punto a = 3.
| |
| − | | |
| − | 6.- Representar de forma conjunta a la gráfica de f(x) y la de esta recta tangente.
| |
| − | Calcula una primitiva de f(x).
| |
| − | | |
| − | '''
| |
| − | Solucion:'''
| |
| − | | |
| − | 1.- Comenzamos definiendo f(x):
| |
| − | ( %i1) f(x):=(x^2-9)/x;
| |
| − | ( %o1)
| |
| − | f (x) :=
| |
| − | <math>x2-9/x</math>
| |
| − | | |
| − | 118 Problema resuelto 1: estudio y representación de una función
| |
| − | Sus puntos de corte con OX verifican f(x) = 0:
| |
| − | ( %i2) solve(f(x)=0,x);
| |
| − | ( %o2)
| |
| − | [x = 3; x = 3]
| |
| − | así que tenemos (3; 0) y (3; 0). Los puntos de corte con OY verifican x = 0, pero
| |
| − | ( %i3) f(0);
| |
| − | Division by 0
| |
| − | #0: f(x=0)
| |
| − | - an error. Quitting. To debug this try debugmode(true);
| |
| − | Evidentemente, el punto x = 0 no está en el dominio, pues el denominador se hace cero
| |
| − | (y Maxima nos da el error anterior).
| |
| − | Valores de f(n)
| |
| − | Podríamos calcular uno a uno los valores de f(n) pero es más rápido, como
| |
| − | vimos en el tema anterior, utilizar la función “map”, que es especialmente apropiada
| |
| − | para crear tablas de valores:
| |
| − | ( %i4) lista:makelist(100*n,n,1,15);
| |
| − | ( %o4)
| |
| − | [100; 200; 300; 400; 500; 600; 700; 800; 900; 1000; 1100; 1200; 1300; 1400; 1500] | |
| − | ( %i5) tabla:map(f,lista);
| |
| − | ( %o5)
| |
| − | �9991
| |
| − | 100
| |
| − | ;
| |
| − | 39991
| |
| − | 200
| |
| − | ;
| |
| − | 29997
| |
| − | 100
| |
| − | ;
| |
| − | 159991
| |
| − | 400
| |
| − | ;
| |
| − | 249991
| |
| − | 500
| |
| − | ;
| |
| − | 119997
| |
| − | 200
| |
| − | ;
| |
| − | 489991
| |
| − | 700
| |
| − | ;
| |
| − | 639991
| |
| − | 800
| |
| − | ;
| |
| − | 89999
| |
| − | 100
| |
| − | ;
| |
| − | 999991
| |
| − | 1000
| |
| − | ;
| |
| − | 1209991
| |
| − | 1100
| |
| − | ;
| |
| − | 479997
| |
| − | 400
| |
| − | ;
| |
| − | 16899130( %i6) %,numer;
| |
| − | ( %o6)
| |
| − | [99;909999999999997; 199;95500000000001; 299;97000000000003; 399;97750000000002; 499;982000000000Parece que | |
| − | l��m
| |
| − | x!+1
| |
| − | f(x) = +1;
| |
| − | pero es mejor confirmarlo con Maxima. Efectivamente:
| |
| − | 119
| |
| − | ( %i7) limit(f(x),x,inf);
| |
| − | ( %o7)
| |
| − | 1
| |
| − | Asíntotas
| |
| − | Como vemos a continuación, f(x) tiene una asíntota vertical en x = 0, de hecho
| |
| − | l��m
| |
| − | x!0+
| |
| − | f(x) = 1 l��m
| |
| − | x!0
| |
| − | f(x) = +1
| |
| − | ( %i8) limit(f(x),x,0);
| |
| − | ( %o8)
| |
| − | und
| |
| − | ( %i9) limit(f(x),x,0,plus);
| |
| − | ( %o9)
| |
| − | 1
| |
| − | ( %i10) limit(f(x),x,0,minus);
| |
| − | ( %o10)
| |
| − | 1
| |
| − | Por otra parte, f(x) no tiene asíntotas horizontales en +1(como vimos, el límite
| |
| − | es +1) y tampoco en 1, como vemos ahora:
| |
| − | ( %i11) limit(f(x),x,minf);
| |
| − | ( %o11)
| |
| − | 1
| |
| − | Y, por otro lado, puesto que
| |
| − | ( %i12) limit(f(x)/x,x,inf);
| |
| − | ( %o12)
| |
| − | 1
| |
| − | f(x) tiene una asíntota oblicua, de la forma y = 1 � x + a, donde a viene dado por el
| |
| − | siguiente límite:
| |
| − | 120 Problema resuelto 1: estudio y representación de una función
| |
| − | ( %i13) limit(f(x)-1*x,x,inf);
| |
| − | ( %o13)
| |
| − | 0
| |
| − | Por tanto, la asíntota oblicua es y = x.
| |
| − | Gráfica
| |
| − | Representaremos f(x) junto con su asíntota, y = x. A base de prueba y error, se
| |
| − | encontrarán los intervalos de x e y adecuados, en este caso se tomará x 2 [20; 20],
| |
| − | y 2 [20; 100]:
| |
| − | ( %i14) plot2d([f(x),x],[x,-20,20],[y,-20,20],[gnuplot_preamble,"set
| |
| − | zeroaxis;"]);
| |
| − | ( %o14)
| |
| − | Figura A.1: Gráfica de la función x29
| |
| − | 2 junto a su asíntota oblicua y = x
| |
| − | Derivada y recta tangente
| |
| − | A continuación, calculamos la derivada de f(x), definimos el punto a = 3 y
| |
| − | hallamos f0(a).
| |
| − | ( %i15) diff(f(x),x);
| |
| − | ( %o15)
| |
| − | 2
| |
| − | x2 9
| |
| − | x2
| |
| − | 121
| |
| − | ( %i16) ratsimp(%);
| |
| − | ( %o16)
| |
| − | x2 + 9
| |
| − | x2
| |
| − | ( %i17) a:3;
| |
| − | ( %o17)
| |
| − | 3
| |
| − | ( %i18) ”(diff(f(x),x)),x=a;
| |
| − | ( %o18)
| |
| − | 2
| |
| − | Obsérvese que (como se comentó en los apuntes de este tema) antes de sustituir el valor
| |
| − | x = a en la derivada, es necesario utilizar un doble operador comilla (”), que se obtiene
| |
| − | pulsando dos veces en la tecla ?. Este operador se puede interpretar como «el resultado
| |
| − | de evaluar la siguiente expresión» (en este caso, la derivada de f(x)). En general, la
| |
| − | última entrada se puede interpretar como «sustituir x = a en el resultado de calcular la
| |
| − | derivada de f(x)».
| |
| − | También podríamos haber utilizado este operador para definir una función, a la que
| |
| − | podríamos llamar Df(x), que representaría a la primera derivada de f(x). Esto lo haremos
| |
| − | más abajo, como ejemplo. Y como se puede ver aprovecharemos para simplificar la
| |
| − | derivada (con la función “ratsimp” antes de definir Df(x)). Así, la definición se puede
| |
| − | leer como «Df(x) se define como el resultado (doble comilla) de simplificar (ratsimp)
| |
| − | la derivada (diff ) de f(x)»
| |
| − | Una vez que conocemos la pendiente, m = f0(a) = 2, podemos escribir la recta
| |
| − | tangente como
| |
| − | y f(a) = m � (x a)
| |
| − | ( %i19) Df(x):=”(ratsimp(diff(f(x),x)));
| |
| − | ( %o19)
| |
| − | Df (x) :=
| |
| − | x2 + 9
| |
| − | x2
| |
| − | ( %i20) m:Df(a);
| |
| − | ( %o20)
| |
| − | 2
| |
| − | ( %i21) y-f(a)=m*(x-a);
| |
| − | ( %o21)
| |
| − | y = 2 (x 3)
| |
| − | 122 Problema resuelto 1: estudio y representación de una función
| |
| − | ( %i22) expand(%);
| |
| − | ( %o22)
| |
| − | y = 2 x 6
| |
| − | Y (utilizando el menú de wxMaxima, si así lo deseamos), podemos representar la
| |
| − | gráfica:
| |
| − | ( %i23) plot2d([f(x),2*x-6],[x,-20,20],[y,-20,20],[gnuplot_preamble,"set
| |
| − | zeroaxis;"]);
| |
| − | ( %o23)
| |
| − | El resultado se puede apreciar en la figura A.2
| |
| − | Figura A.2: Gráfica de la función x29
| |
| − | 2 junto su recta tengente en x = 3
| |
| − | Primitiva y área
| |
| − | Calcular una primitiva es fácil. Recurramos o no al sistema de menús de wxMaxima,
| |
| − | tendremos:
| |
| − | ( %i24) integrate(f(x),x);
| |
| − | ( %o24)
| |
| − | x2
| |
| − | 2 9 log x
| |
| − | Para el cálculo de áreas, observamos que f(x) > 0 en [3;+1), pues hemos visto que
| |
| − | f(3) = 0 y si x > 3 el numerador y el denominador de f(x) son estrictamente positivos
| |
| − | 123
| |
| − | | |
| − | Sus puntos de corte con OX verifican f(x) = 0:
| |
| − | ( %i2) solve(f(x)=0,x);
| |
| − | ( %o2)
| |
| − | [x = -3; x = 3]
| |