Diferencia entre revisiones de «2010 Ejercicios de introducción a Maxima»
De Software Libre para la Enseñanza y el Aprendizaje de las Matemáticas (2010-11)
(→Ejercicio 6.1) |
(→Ejercicio 2) |
||
| Línea 25: | Línea 25: | ||
'''Solución:''' | '''Solución:''' | ||
| + | (%i1)radcan ((sin(%pi/3)+cos(%pi/3))^9); | ||
| + | (%01)(17*3^(5/2)+265)/32) | ||
== Ejercicio 3 == | == Ejercicio 3 == | ||
Revisión del 16:57 28 abr 2010
Fonciones y variables a utilizar: float, is, expand, fpprec, bfloat, solve, factor, rectform, abs, carg, plot2D y find_root.
Sumario
Ejercicio 1
Ejercicio 1.1
Definir la constante <math>a = (20+14\sqrt{2})^{1/3} + (20-14\sqrt{2})^{1/3}</math>.
Solución:
(%i1) a : (20+14*sqrt(2))^(1/3) + (20-14*sqrt(2))^(1/3); (%o1) (7*2^(3/2)+20)^(1/3)+(20-7*2^(3/2))^(1/3)
Ejercicio 1.2
Calcular el valor numérico de a. ¿A qué entero se aproxima?
Solución:
(%i2) float(a); (%o2) 3.999999999999996 (%i3) round(%); (%o3) 4
Ejercicio 2
Ejercicio 2. Escribir el número <math>\left(sin\frac{\pi}{3}+cos\frac{\pi}{3}\right)^9</math> en la forma <math>a + b \ast c^d</math>, donde <math>a, b, c</math> y <math>d</math> son números racionales.
Nota: Cambiar el valor de la variable %piargs a true y usar radcan para la simplificación de radicales.
Solución:
(%i1)radcan ((sin(%pi/3)+cos(%pi/3))^9); (%01)(17*3^(5/2)+265)/32)
Ejercicio 3
Calcular la cifra 149 del número <math>\pi</math>.
Solución:
(%i1) fpprec : 149;bfloat(%pi); (%o1) 149 (%o2) 3.1415926535897932384626433832[92 digits]0938446095505822317253594081b0
Ejercicio 4
Se considera el polinomio <math>p = x^4-x^3-7x^2-8x-6</math>.
(%i1) p:x^4-x^3-7*x^2-8*x-6; (%o1) x^4-x^3-7*x^2-8*x-6
Ejercicio 4.1.
Calcular las raices reales de <math>p</math>.
Solución:
(%i2) realroots(p); (%o2) [x=-55222251/33554432,x=122331115/33554432]
Ejercicio 4.2
Factorizar al máximo el polinomio <math>p</math>.
Solución:
(%i3) factor(p); (%o3) (x^2-2*x-6)*(x^2+x+1)
Ejercicio 5
Sea <math>z=\left(\frac{1-i\sqrt 3}{1+i}\right)^{20}</math>.
(%i1) z: ((1-%i*sqrt(3))/(1+%i))^20$
Ejercicio 5.1
Calcular la parte real y la parte imaginaria de <math>z</math>.
Solución:
(%i2) realpart(z); (%o2) 512
(%i3) imagpart(z)$ (%i4) radcan(%); (%o4) 512*sqrt(3)
Ejercicio 5.2
Calcular el módulo y el argumento de <math>z</math>.
Solución:
(%i5) ratsimp(abs(z));ratsimp(carg(z)); (%o5) 1024 (%o6) %pi/3
Ejercicio 6
Ejercicio 6.1
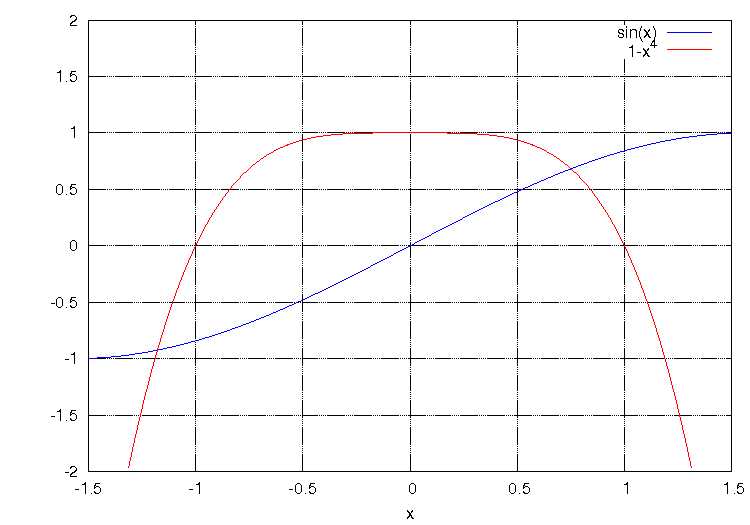
Con la ayuda de la representación gráfica, conjeturar el número de soluciones de la ecuación
- <math>\sin x=1-x^4</math>.
Solución:
(%i1) (%i1) wxplot2d([sin(x),1-x^4], [x,-1.5,1.5], [y,-2,2], [gnuplot_preamble, "set xrange [-1.5:1.5]; set yrange [-2:2]; set grid;"]);
A la vista de la gráfica, la ecuación tendrá 2 soluciones.
Ejercicio 6.2
Dar una aproximación de cada solución.
Solución:
Observando la gráfica podemos estimar que las soluciones serán -1,2 y 0,7.
Ejercicio 7
Resolver el siguiente sistema lineal en función de los parámetros <math>a, b</math> y <math>c</math>:
- <math>
\left\{ \begin{array}{l} x+ay+a^2 z=0 \\ x+by+b^2 z=0 \\ x+cy+c^2z=1 \end{array} \right. </math>
Solución:
(%i1)sist:[x+a*y+a^2*z=0, x+b*y+b^2*z=0, x+c*y+c^2*z=1]$
(%i2)solve(sist, [x,y,z]);
(%o2)[[x=(a*b)/(c^2-b*c+a*(b-c)),
y=-(b+a)/(c^2-b*c+a*(b-c)),
z=1/(c^2-b*c+a*(b-c))]]